DTEAssurance is an R package for implementing
assurance methodology in the design of clinical trials with an
anticipated delayed treatment effect (DTE).
It uses elicited prior distributions—via the SHELF
framework—for the delay duration and post-delay hazard ratio, and
simulates operating characteristics to inform trial design.
The methodology is based on the following papers:
Salsbury JA, Oakley JE, Julious SA, Hampson LV.
Assurance
methods for designing a clinical trial with a delayed treatment
effect.
Statistics in Medicine, 2024; 43(19): 3595–3612. doi:10.1002/sim.10136
Salsbury JA, Oakley JE, Julious SA, Hampson LV.
Adaptive clinical trial
design with delayed treatment effects using elicited prior
distributions.
arXiv preprint, 2025; arXiv:2509.07602 [under revision at
Pharmaceutical Statistics]
You can install DTEAssurance from GitHub using:
# Install from GitHub
devtools::install_github("jamesalsbury/DTEAssurance")
#> Using GitHub PAT from the git credential store.
#> Skipping install of 'DTEAssurance' from a github remote, the SHA1 (da7dd954) has not changed since last install.
#> Use `force = TRUE` to force installation
library(DTEAssurance)Once accepted to CRAN, you’ll be able to install it with:
install.packages("DTEAssurance")
#> Warning: package 'DTEAssurance' is in use and will not be installedShiny AppLaunch the interactive app to explore assurance under delayed treatment effects:
DTEAssurance::assurance_shiny_app()You can also use the package offline via the main function:
DTEAssurance::calc_dte_assurance()This function requires the following arguments:
n_c: Number of patients in the control groupn_t: Number of patients in the treatment groupcontrol_model: A named list specifying the control arm
survival distributioneffect_model: A named list specifying beliefs about the
treatment effectcensoring_model: A named list specifying the censoring
mechanismrecruitment_model: A named list specifying the
recruitment processanalysis_model: A named list specifying the statistical
test and decision rulen_sims: Number of simulations to runAn example of this is shown:
control_model <- list(dist = "Exponential", parameter_mode = "Fixed", fixed_type = "Parameters", lambda = 0.1)
effect_model <- list(delay_SHELF = SHELF::fitdist(c(3, 4, 5), probs = c(0.25, 0.5, 0.75), lower = 0, upper = 10),
delay_dist = "gamma",
HR_SHELF = SHELF::fitdist(c(0.55, 0.6, 0.7), probs = c(0.25, 0.5, 0.75), lower = 0, upper = 1.5),
HR_dist = "gamma",
P_S = 1, P_DTE = 0)
censoring_model <- list(method = "Time", time = 12)
recruitment_model <- list(method = "power", period = 12, power = 1)
analysis_model <- list(method = "LRT", alpha = 0.025, alternative_hypothesis = "one.sided")
result <- calc_dte_assurance(n_c = 300, n_t = 300,
control_model = control_model,
effect_model = effect_model,
censoring_model = censoring_model,
recruitment_model = recruitment_model,
analysis_model = analysis_model,
n_sims = 100)
str(result)
#> List of 4
#> $ assurance : num 0.83
#> $ CI : num [1, 1:2] 0.742 0.898
#> $ duration : num 12
#> $ sample_size: num 600We can vary the sample sizes and plot the resulting output:
result <- calc_dte_assurance(n_c = seq(50, 500, by = 50),
n_t = seq(50, 500, by = 50),
control_model = control_model,
effect_model = effect_model,
censoring_model = censoring_model,
recruitment_model = recruitment_model,
analysis_model = analysis_model,
n_sims = 500)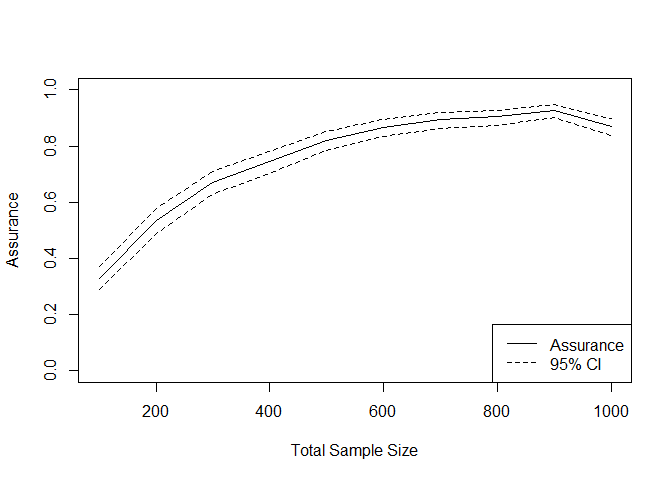
Shiny AppLaunch the interactive shiny app to explore assurance
under delayed treatment effects using group sequential designs:
DTEAssurance::assurance_GSD_shiny_app()You can also use the package offline via the main function:
DTEAssurance::calc_dte_assurance_interim()This function requires the following arguments:
n_c: Number of patients in the control groupn_t: Number of patients in the treatment groupcontrol_model: A named list specifying the control arm
survival distributioneffect_model: A named list specifying beliefs about the
treatment effectrecruitment_model: A named list specifying the
recruitment processGSD_model: A named list specifying the group sequential
designn_sims: Number of simulations to runAn example of this is shown:
control_model <- list(dist = "Exponential", parameter_mode = "Fixed", fixed_type = "Parameters", lambda = 0.08)
effect_model <- list(delay_SHELF = SHELF::fitdist(c(3, 4, 5), probs = c(0.25, 0.5, 0.75), lower = 0, upper = 10),
delay_dist = "gamma",
HR_SHELF = SHELF::fitdist(c(0.55, 0.6, 0.7), probs = c(0.25, 0.5, 0.75), lower = 0, upper = 1.5),
HR_dist = "gamma",
P_S = 0.9, P_DTE = 0.7)
recruitment_model <- list(method = "power", period = 12, power = 1)
GSD_model <- list(events = 450, alpha_spending = c("0.01, 0.025"),
beta_spending = c("0.05, 0.1"), IF_vec = c("0.5, 1"))
result <- calc_dte_assurance_interim(n_c = 300, n_t = 300,
control_model = control_model,
effect_model = effect_model,
recruitment_model = recruitment_model,
GSD_model = GSD_model,
n_sims = 500)
str(result)
#> 'data.frame': 500 obs. of 6 variables:
#> $ Trial : int 1 2 3 4 5 6 7 8 9 10 ...
#> $ IF : chr "0.5, 1" "0.5, 1" "0.5, 1" "0.5, 1" ...
#> $ Decision : chr "Successful at final" "Stop for efficacy" "Stop for futility" "Stop for futility" ...
#> $ StopTime : num 27.1 13.6 12.5 12.9 13.7 ...
#> $ SampleSize : int 600 600 600 600 600 600 600 600 600 600 ...
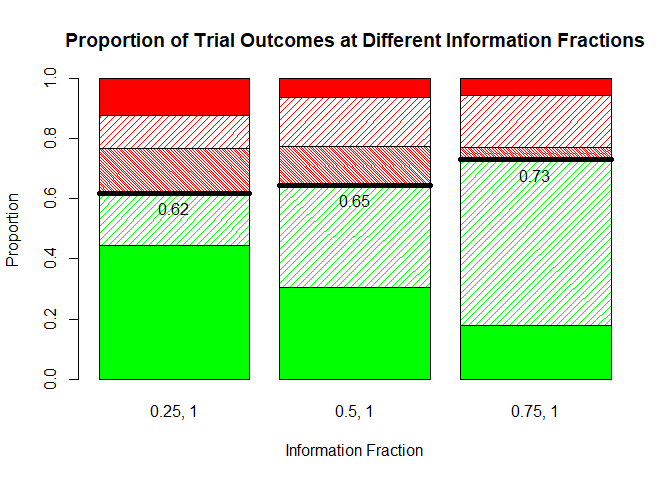
#> $ Final_Decision: chr "Successful" "Successful" "Successful" "Successful" ...If we wish to compare the operating characteristics we can do so by
changing the GSD_model and plotting the proportion of
outcomes:
GSD_model <- list(events = 450,
alpha_spending = c("0.01, 0.025", "0.01, 0.025", "0.01, 0.025"),
beta_spending = c("0.05, 0.1", "0.05, 0.1", "0.05, 0.1"),
IF_vec = c("0.25, 1", "0.5, 1", "0.75, 1"))
result <- calc_dte_assurance_interim(n_c = 300, n_t = 300,
control_model = control_model,
effect_model = effect_model,
recruitment_model = recruitment_model,
GSD_model = GSD_model,
n_sims = 500)