

The weird package contains functions and data used in the book That’s Weird: Anomaly Detection Using R by Rob J Hyndman. It also loads several packages needed to do the analysis described in the book.
You can install the development version of weird from GitHub with:
# install.packages("devtools")
devtools::install_github("robjhyndman/weird-package")library(weird) will load the following packages:
You also get a condensed summary of conflicts with other packages you have loaded:
library(weird)
#> ── Attaching packages ────────────────────────────────────── weird 0.0.0.9000 ──
#> ✔ dplyr 1.1.4 ✔ ks 1.14.1
#> ✔ ggplot2 3.4.4
#> ── Conflicts ──────────────────────────────────────────────── weird_conflicts ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag() masks stats::lag()The oldfaithful data set contains eruption data from the
Old Faithful Geyser in Yellowstone National Park, Wyoming, USA, from 1
January 2015 to 1 October 2021. The data were obtained from the geysertimes.org website. Recordings
are incomplete, especially during the winter months when observers may
not be present. There also appear to be some recording errors. The data
set contains 2261 observations of 3 variables: time giving
the time at which each eruption began, duration giving the
length of the eruption in seconds, and waiting giving the
time to the next eruption in seconds. In the analysis below, we omit the
eruption with duration greater than 1 hour as this is
likely to be a recording error. Some of the long waiting
values are probably due to omitted eruptions, and so we also omit
eruptions with waiting greater than 2 hours.
oldfaithful
#> # A tibble: 2,261 × 3
#> time duration waiting
#> <dttm> <dbl> <dbl>
#> 1 2015-01-02 14:53:00 271 5040
#> 2 2015-01-09 23:55:00 247 6060
#> 3 2015-02-07 00:49:00 203 5460
#> 4 2015-02-14 01:09:00 195 5221
#> 5 2015-02-21 01:12:00 210 5401
#> 6 2015-02-28 01:11:00 185 5520
#> 7 2015-03-07 00:50:00 160 5281
#> 8 2015-03-13 21:57:00 226 6000
#> 9 2015-03-13 23:37:00 190 5341
#> 10 2015-03-20 22:26:00 102 3961
#> # ℹ 2,251 more rowsThe package provides the kde_bandwidth() function for
estimating the bandwidth of a kernel density estimate, and an
autoplot() method for plotting the resulting density. The
figure below shows the kernel density estimate of the
duration variable obtained using these functions. The rug
plot shows the actual data values.
of <- oldfaithful |>
filter(duration < 3600, waiting < 7200)
of_density <- kde(of$duration, h=kde_bandwidth(of$duration))
of_density |>
autoplot() +
geom_rug(aes(x=duration), of) +
labs(x = "Duration (seconds)")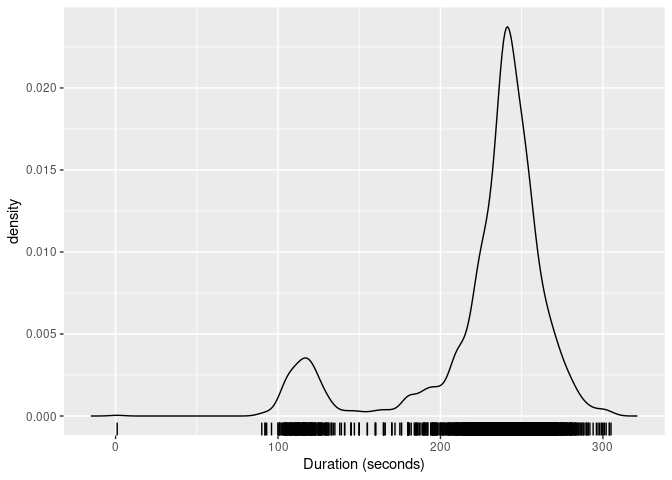
The kde_bandwidth() function can also be used to
estimate the bandwidth for a bivariate kernel density estimate. The
figure below shows the kernel density estimate of the
duration and waiting variables using the
bandwidth selected by the kde_bandwidth() function. The rug
plot shows the actual data values.
of_density <- of |>
select(duration, waiting) |>
kde(H = kde_bandwidth(of[,c("duration","waiting")]))
of_density |>
autoplot() +
geom_point(aes(duration, waiting), data = of, alpha=0.15) +
labs(x = "Duration (seconds)", y = "Waiting time (seconds)")
Some old methods of anomaly detection used statistical tests. While these are not recommended, they are still widely used, and are provided in the package for comparison purposes.
of |> filter(peirce_anomalies(duration))
#> # A tibble: 1 × 3
#> time duration waiting
#> <dttm> <dbl> <dbl>
#> 1 2018-04-25 19:08:00 1 5700
of |> filter(chauvenet_anomalies(duration))
#> # A tibble: 1 × 3
#> time duration waiting
#> <dttm> <dbl> <dbl>
#> 1 2018-04-25 19:08:00 1 5700
of |> filter(grubbs_anomalies(duration))
#> # A tibble: 1 × 3
#> time duration waiting
#> <dttm> <dbl> <dbl>
#> 1 2018-04-25 19:08:00 1 5700
of |> filter(dixon_anomalies(duration))
#> # A tibble: 1 × 3
#> time duration waiting
#> <dttm> <dbl> <dbl>
#> 1 2018-04-25 19:08:00 1 5700In this example, they only detect the tiny 1-second duration, which is almost certainly a recording error. An explanation of these tests is provided in Chapter 4 of the book
Boxplots are widely used for anomaly detection. Here are three
variations of boxplots applied to the duration
variable.
of |>
ggplot(aes(x = duration)) +
geom_boxplot() +
scale_y_discrete() +
labs(y = "", x = "Duration (seconds)")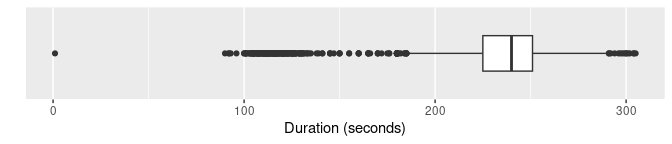
of |> gg_hdrboxplot(duration) +
labs(x = "Duration (seconds)")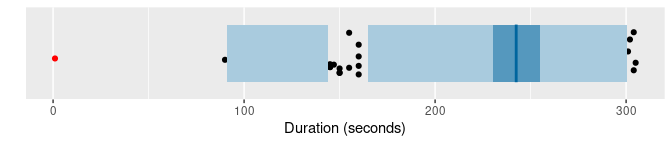
of |> gg_hdrboxplot(duration, scatterplot = TRUE) +
labs(x = "Duration (seconds)")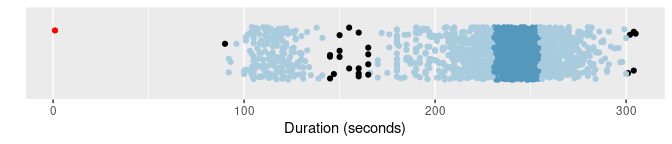
The latter two plots are HDR boxplots, which allow the bimodality of the data to be seen. The dark shaded region contains 50% of the observations, while the lighter shaded region contains 99% of the observations. The plots use vertical jittering to reduce overplotting, and highlight potential outliers in red using the lookout algorithm (described in Chapter 6 of the book). An explanation of these plots is provided in Chapter 5 of the book.
It is also possible to produce bivariate boxplots. Several variations are provided in the package. Here are two types of bagplot.
of |>
gg_bagplot(duration, waiting) +
labs(x = "Duration (seconds)", y = "Waiting time (seconds)")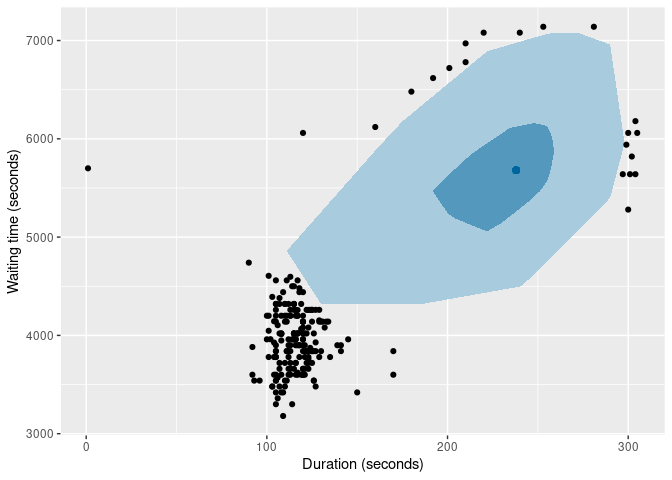
of |>
gg_bagplot(duration, waiting, scatterplot = TRUE) +
labs(x = "Duration (seconds)", y = "Waiting time (seconds)")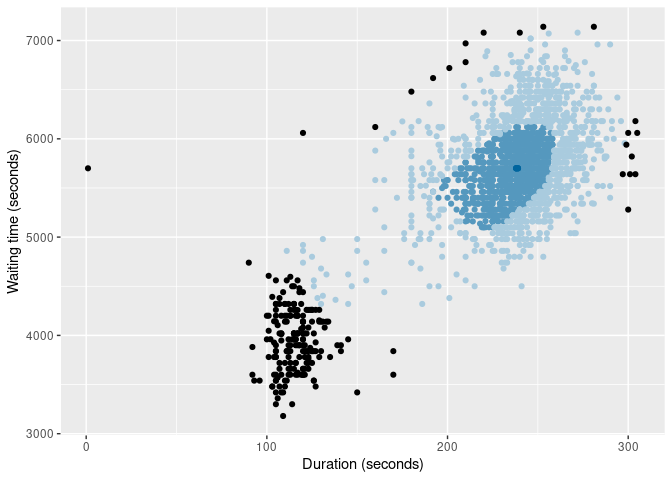
And here are two types of HDR boxplot
of |>
gg_hdrboxplot(duration, waiting) +
labs(x = "Duration (seconds)", y = "Waiting time (seconds)") 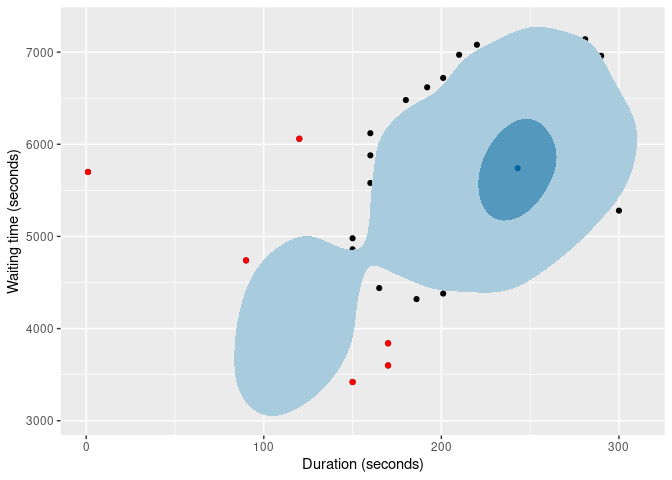
of |>
gg_hdrboxplot(duration, waiting, scatterplot = TRUE) +
labs(x = "Duration (seconds)", y = "Waiting time (seconds)") 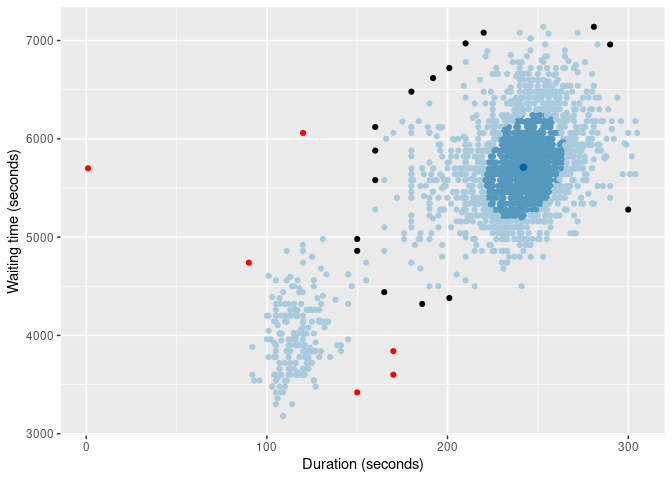
The latter two plots show likely outliers in red, using the lookout algorithm.
Several functions are provided for providing anomaly scores for all observations.
density_scores() function uses either a fitted
statistical model, or a kernel density estimate, to compute density
scores.stray_scores() function uses the stray algorithm to
compute anomaly scores.lof_scores() function uses local outlier factors to
compute anomaly scores.glosh_scores() function uses the Global-Local
Outlier Score from Hierarchies algorithm to compute anomaly scores.lookout() function uses the lookout algorithm to
compute anomaly probabilitiesHere are the top 0.02% most anomalous observations identified by each of the first four methods, along with the observations having lookout probability less than 0.05.
of |>
mutate(
denscore = density_scores(cbind(duration, waiting)),
strayscore = stray_scores(cbind(duration, waiting)),
lofscore = lof_scores(cbind(duration, waiting), k = 150),
gloshscore = glosh_scores(cbind(duration, waiting)),
lookout = lookout(cbind(duration, waiting))
) |>
filter(
denscore > quantile(denscore, prob=0.998) |
strayscore > quantile(strayscore, prob=0.998) |
lofscore > quantile(lofscore, prob=0.998) |
gloshscore > quantile(gloshscore, prob=0.998) |
lookout < 0.05
) |>
arrange(lookout)
#> # A tibble: 11 × 8
#> time duration waiting denscore strayscore lofscore gloshscore
#> <dttm> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 2018-04-25 19:08:00 1 5700 17.5 0.380 3.78 1
#> 2 2020-06-01 21:04:00 120 6060 17.5 0.132 1.88 1
#> 3 2021-01-22 18:35:00 170 3600 16.8 0.0606 1.09 0.860
#> 4 2020-08-31 09:56:00 170 3840 16.7 0.0606 1.01 0.816
#> 5 2015-11-21 20:27:00 150 3420 16.7 0.0772 1.27 1
#> 6 2017-05-03 06:19:00 90 4740 16.4 0.0495 1.68 1
#> 7 2020-10-15 17:11:00 220 7080 15.7 0.0429 2.42 1
#> 8 2017-09-22 18:51:00 281 7140 15.5 0.0333 2.64 1
#> 9 2017-08-12 13:14:00 120 4920 15.2 0.0690 1.53 1
#> 10 2020-05-18 21:21:00 272 7080 14.9 0.0333 2.42 1
#> 11 2018-09-22 16:37:00 253 7140 14.7 0.0200 2.63 1
#> # ℹ 1 more variable: lookout <dbl>Some anomaly detection methods require the data to be scaled first,
so all observations are on the same scale. However, many scaling methods
are not robust to anomalies. The mvscale() function
provides a multivariate robust scaling method, that optionally takes
account of the relationships betwen variables, and uses robust estimates
of center, scale and covariance by default. The centers are removed
using medians, the scale function is the IQR, and the covariance matrix
is estimated using a robust OGK estimate. The data are scaled using the
Cholesky decomposition of the inverse covariance. Then the scaled data
are returned. The scaled variables are rotated to be orthogonal, so are
renamed as z1, z2, etc. Non-rotated scaling is
possible by setting cov = NULL.
mvscale(of)
#> Warning in mvscale(of): Ignoring non-numeric columns: time
#> # A tibble: 2,197 × 3
#> time z1 z2
#> <dttm> <dbl> <dbl>
#> 1 2015-01-02 14:53:00 2.06 -1.47
#> 2 2015-01-09 23:55:00 0.130 0.801
#> 3 2015-02-07 00:49:00 -1.78 -0.534
#> 4 2015-02-14 01:09:00 -2.04 -1.07
#> 5 2015-02-21 01:12:00 -1.38 -0.665
#> 6 2015-02-28 01:11:00 -2.76 -0.401
#> 7 2015-03-07 00:50:00 -3.92 -0.932
#> 8 2015-03-13 21:57:00 -0.932 0.668
#> 9 2015-03-13 23:37:00 -2.38 -0.799
#> 10 2015-03-20 22:26:00 -6.09 -3.87
#> # ℹ 2,187 more rows
mvscale(of, cov = NULL)
#> Warning in mvscale(of, cov = NULL): Ignoring non-numeric columns: time
#> # A tibble: 2,197 × 3
#> time duration waiting
#> <dttm> <dbl> <dbl>
#> 1 2015-01-02 14:53:00 1.61 -1.48
#> 2 2015-01-09 23:55:00 0.363 0.809
#> 3 2015-02-07 00:49:00 -1.92 -0.540
#> 4 2015-02-14 01:09:00 -2.33 -1.08
#> 5 2015-02-21 01:12:00 -1.56 -0.672
#> 6 2015-02-28 01:11:00 -2.85 -0.405
#> 7 2015-03-07 00:50:00 -4.15 -0.942
#> 8 2015-03-13 21:57:00 -0.726 0.674
#> 9 2015-03-13 23:37:00 -2.59 -0.807
#> 10 2015-03-20 22:26:00 -7.16 -3.91
#> # ℹ 2,187 more rows